Как удержать козу в треугольнике

Опубликовано: 23.04.2024

Ответ. Нужно привязать её верёвкой, длина которой равна радиусу этого круга, за колышек, стоящий в его центре. Тогда, чтобы выйти за пределы круга, козе не хватит длины верёвки, потому что все точки вне круга удалены от его центра на расстояние, большее, чем его радиус (а значит, и чем длина верёвки). И наоборот, все точки круга расположены на не большем расстоянии от его центра, чем его радиус, поэтому коза сможет съесть всё внутри круга.

Ответ. В круге радиуса 1м вокруг любой точки любой стороны прямоугольника всё будет съедено (на рисунке показаны примеры таких кругов). Внешняя граница фигуры будет представлять собой прямоугольник со скругленными углами (поглядев на рисунок внимательнее, вы поймёте, почему радиус скругления равен 1м) и со сторонами 3 + 1 + 1 = 5 и 5 + 1 + 1 = 7 метров. Внутренняя граница — это уже обычный прямоугольник со сторонами 3 - 1 - 1 = 1 и 5 - 1 - 1 = 3 метров.

4. Привяжите козу с помощью веревок и колышков так, чтобы она могла съесть траву только внутри участка такой формы:

Ответ. Эта область — пересечение двух кругов. Привяжем козу как в первой задаче, чтобы она не могла выйти из первого круга, к центру первого круга на верёвке, длина которой равна радиусу этого круга. Одновременно с этим привяжем козу другой верёвкой, длина которой равна радиусу второго круга, к центру этого круга. В итоге коза не сможет выйти из первого круга, потому что привязана к его центру, и из второго круга, потому что привязана и к его центру. То есть, она всегда будет находится в пересечении этих двух кругов. (Определение и рисунок пересечения множеств можно найти тут.)
Примечание: вообще, чтобы коза не выходила из пересечения каких-либо двух множеств, достаточно (хотя и не обязательно, ведь могут быть способы добиться этого по-другому) привязать её так, чтобы она не выходила из первого, и чтобы не выходила из второго, то есть решить две независимые задачи.

Ответ. На расстоянии, равном длине второй верёвки, от каждой точки первой верёвки, всё будет съедено. Таким образом, будут выедены круги, центры которых находятся на отрезке между двумя колышками (на рисунке показаны примеры нескольких таких кругов). Их объединение образует фигуру, состоящую из прямоугольника и двух полукругов (её также можно назвать прямоугольником со скругленными углами, радиус скругления которых равен ширине прямоугольника и равен длине второй верёвки, а длина прямоугольника равна длине первой верёвки плюс удвоенная длина второй верёвки).

а)Сначала привяжем козу так, чтобы она не выходила из полного круга. Нужно добавить ещё верёвки, чтобы удержать её в нужной половине. Эта часть границы полукруга является отрезком прямой, а такая граница была у нас до этого в задаче 5. Поэтому привяжем её дополнительно таким же образом, как в той задаче. Итак, можно представить полукруг как пересечение круга и фигуры, получившейся в задаче 5. Ещё можно заменить фигуру 5 прямоугольником.

б)Квадрат — пересечение двух фигур из задачи 5, для которых длины вторых верёвок одинаковы.

в)Прямоугольник тоже можно представить как пересечение двух таких фигур, а можно придумать другую систему верёвок, где одна верёвка будет скользить на петлях по двум направляющим, а коза будет привязана к ней за ошейник так, что сможет ходить вдоль этой верёвки.

Пусть А - область, доступная козе без учёта собак, В - области, доступные собакам. Тогда заметим, что коза не сможет выйти из разности множеств А\В (по определению, точка принадлежит А\В тогда и только тогда, когда она принадлежит А, но не принадлежит В, что в точности повторяет определение действия собак на козу).

а) Кольцо представляет собой разность двух кругов, имеющих один и тот же центр. Значит, козу надо привязать так, чтобы она ходила по большему кругу, а собаку — по меньшему.

б) Полукруг можно представить как разность круга и прямоугольника или круга и фигуры из задачи 5. А можно решить эту задачу иначе, пустив собаку вдоль натянутой по диаметру круга верёвки и разделив тем самым круг на две разные части. Тогда коза не сможет перейти в другую часть круга и останется в том полукруге, где была изначально. (Кстати, в этом примере видно, что коза не обязательно будет ходить по всей разности множеств, которая в данном случае представляет собой весь круг без отрезка, ведь она разделена на несколько не связанных между собой частей.)

Занятие 1
Занятие посвящено козам. Они прожорливые и съедают все, до чего могут дотянуться. Поэтому коз держат на привязи.

1. Нарисуйте участок луга, который выест коза, привязанная веревкой к одиноко стоящему на лугу колышку.

2. Математик прогуливался по лугу, держа козу на поводке длины 1м. Путь математика имел вид
а) отрезка длины 3
б) прямоугольника размером 3 м х 5 м.
Нарисуйте участок, на котором могла побывать при этом коза, не обрывая поводка.

3. Удержите козу на участке такой формы: (привяжите ее с помощью веревок и колышков так, чтобы она могла есть траву лишь внутри этого участка — рис.1).

4. На лугу между двумя колышками натянем веревку. У второй веревки один конец привяжем к ошейнику козы, а на другом сделаем петлю, скользящую по первой веревке. Какой участок выест коза?

5. Удержите козу
а) в полукруге;
б) в квадрате;
в) в данном прямоугольнике.

6. Удержите козу
а) в треугольнике;
б) в равностороннем шестиугольнике.

7. Удержите козу при помощи собак
а) в кольце
б) в фигуре, изображенной на рисунке 2.

8. Удержите не привязанную козу при помощи собак в фигуре, изображенной на рисунке 3.

1. Найти площади многоугольников, изображенных на рисунке, если площадь одной клетки равна 1:

2. Нарисуйте квадрат с вершинами в узлах сетки, площадь которого
а) 4, б) 13, в) 26, г) 40.

3. Нарисуйте прямоугольник с вершинами в узлах сетки, стороны которого не равны 2 и 5, а площадь равна 10.

4. Может ли площадь многоугольника с вершинами в узлах сетки быть равна:
а) 3, б) 1/2, в) 10/3, г) 15/3, д) 1/10

Если может, привести пример фигуры; если не может объяснить почему?

5. Доказательство теоремы Пифагора, придуманное математиком Ариабхате, жившего в 476-550гг.

1. Из 9 монет одна — фальшивая, она тяжелее настоящих. Найти ее за два взвешивания.

2. Из 27 монет одна — фальшивая, она легче настоящих. Можно ли найти ее за:
а) 3 взвешивания
б) 2 взвешивания.

3. Есть 6 монет, из которых две — фальшивые (легче настоящих). Найти их за 3 взвешивания.

4. Имеется 101 монета. Из них 100 одинаковых настоящих монет и одна фальшивая, отличающаяся по весу. Необходимо определить, легче или тяжелее фальшивая монета, чем настоящая. Как это сделать при помощи двух взвешиваний на чашечных весах без гирь?

5. Из 101 монеты 50 — фальшивые, которые на 1 грамм легче настоящих. За одно взвешивание на весах с делениями определить, является ли данная монета фальшивой.

6. Есть 5 монет, из которых три настоящих, две фальшивых, одна из которых тяжелее настоящей, а другая легче. За три взвешивания на чашечных весах определите обе фальшивые монеты.

7. Из 103 монет две — фальшивые (фальшивые монеты одинаковы по весу). За три взвешивания определить, тяжелее они настоящих или легче.

8. Из 16 монет одна — фальшивая, причем неизвестно, легче она настоящих или тяжелее. Найти ее за 4 взвешивания.

9. Из 12 монет одна — фальшивая, причем неизвестно, легче она настоящих или тяжелее. Найти ее за 3 взвешивания.

10. Есть 6 мешков с монетами. В некоторых из них монеты фальшивые (на 1 грамм легче настоящих). За одно взвешивание на весах с делениями определить, в каких мешках монеты фальшивые, если известно, что:
а) Фальшивые монеты только в одном мешке.
б) Фальшивые монеты не во всех мешках.

11. Имеется 6 мешков, в каждом из которых лежит много гирек. Известно, что в каждом мешке гирьки одинаковые и весят целое число граммов от 1 до 10. За какое наименьшее число взвешиваний на точных цифровых весах можно определить вес гирьки каждого типа?

1. Через точку внутри треугольника проведены прямые, параллельные трем сторонам треугольника. Эти прямые разбивают исходный треугольник на три треугольника и три параллелограмма. Произведение площадей полученных треугольников равно а. Найти произведение площадей параллелограммов.

2. Через точку внутри треугольника проведены три прямые, параллельные сторонам; они делят треугольник на шесть частей, три из которых – параллелограммы. Площади этих параллелограммов равны П1, П2, П3. Найдите площадь треугольника.

3. Точка, произвольно взятая внутри равностороннего треугольника, соединена со всеми вершинами. Кроме того, из нее опущены перпендикуляры на все стороны треугольника. Докажите, что сумма площадей закрашенных треугольников равна сумме площадей незакрашенных треугольников (рис.4).

4. Две прямые делят каждую из двух противоположных сторон выпуклого четырехугольника на три равные части. Докажите, что между этими прямыми заключена треть площади четырехугольника.

5. Все стороны выпуклого треугольника площади 1 разделены на три равные части. Найдите площадь «креста», показанного на рис.5.

6. Дан выпуклый четырехугольник ABCD. K, L, M, N – середины сторон BC, CD, DA и АВ (рис.6). Доказать, что
1) KLMN – параллелограмм;
2) SKLMN = ? SABCD ;
3) S1 + S3 = S2 + S4

7. Каждая сторона выпуклого четырехугольника разделена на четыре равные части. Соответствующие точки деления на противоположных сторонах соединены друг с другом, и полученные клетки раскрашены в шахматном порядке в белый и черный цвета. Докажите, что сумма площадей белых клеток равна сумме площадей черных клеток (рис.7).

Домашнее задание:

1. Нарисуйте 5 прямоугольников с вершинами в узлах сетки, площади которых равны 24.

2. На клетчатой бумаге нарисован прямоугольник с вершинами в узлах клеток. Пусть А – число узлов внутри него, а С – число узлов на границе. Найти площадь прямоугольника.

3. Решить задачу 1 для прямоугольного треугольника, с вершинами в узлах клеток, две стороны которого проходят по линии сетки.

4. Решите задачу 1 для прямоугольного треугольника, с вершинами в узлах клеток, одна сторона которого проходит по линии сетки.

5. Семья ночью пошла по мосту. Папа может перейти его за 1 минуту, мама — за 2, малыш — за 5, бабушка – за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из их скоростей. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя. Орать друг на друга нельзя.)
При составлении задач использованы материалы ВМШ Пятьдесят седьмой школы

Найдите сумму величин углов MAN , MBN , MCN , MDN и MEN , нарисованных на клетчатой бумаге так, как это показано на рисунке справа.

Серёжа придумал фигуру, которую легко разрезать на две части и сложить из них квадрат (см. рис.). Покажите, как по-другому разрезать эту фигуру на две части, из которых тоже можно сложить квадрат.

Пространственное воображение

У Пети есть три фигуры, вырезанные из бумаги. Каждая из них с одной стороны белая, а с другой — серая. Какие из пяти прямоугольников, изображенных на рисунке, нельзя сложить из этих фигур?
а) Тетраэдр б) куб разрезали по ребрам, выделенным жирными линиями (см. рисунки) и развернули. Нарисуйте получившиеся развертки.
На каждом рисунке изображены два различных положения куба с заданной осью поворота (сверху — до поворота, снизу — после поворота). На верхнем кубе отмечены две его вершины, а на нижнем указано положение лишь одной из них. Отметьте положение второй вершины.
На каждом рисунке изображены два различных положения многогранника: куба, тетраэдра или октаэдра. На верхнем рисунке дано его исходное положение, на втором — после некоторого перемещения в пространстве. На первом рисунке отмечены некоторые элементы многогранника. Отметьте их на втором.
Представьте, что куб стоит на столе на одной своей вершине (так, что верхняя вершина расположена точно над нижней) и освещён прямо сверху. Какая в этом случае получается тень от куба? Нарисуйте ее.
Из квадрата 5x5 вырезали центральную клетку. Разрежьте получившуюся фигуру на две части, в которые можно завернуть куб 2x2x2.

Дополнительные задачи

Рисунок к задаче 3.

Рисунок к задаче 4.

Задачи про коз

На сколько градусов поворачивается за одну минуту минутная стрелка? Часовая стрелка? Найдите угол между часовой и минутной стрелками в 3 часа 20 минут.
Через точку на плоскости провели 7 прямых, после чего плоскость разрезали по этим прямым на углы. Верно ли, что хотя бы один из этих углов меньше 26 градусов ?
Имеется угольник с углом в 19 градусов , а другие углы неизвестны. Как построить с его помощью угол в 1 градус?
Можно ли провести из одной точки на плоскости пять лучей так, чтобы среди образованных ими углов было ровно четыре острых? Рассматриваются углы не только между соседними, но и между любыми двумя лучами.
В Совершенном городе шесть площадей. Каждая площадь соединена прямыми улицами ровно с тремя другими площадями. Никакие две улицы в городе не пересекаются. Из трёх улиц, отходящих от каждой площади, одна проходит внутри угла, образованного двумя другими. Начертите возможный план такого города.
Есть три треугольника: остроугольный, прямоугольный и тупоугольный. Саша взял себе один треугольник, а Боря

--- два оставшихся. Оказалось, что Боря может приложить (без наложения) один из своих треугольников к другому, и получить треугольник, равный Сашиному. Какой из этих треугольников взял Саша?

Придумайте комнату такой формы, чтобы в ней можно было указать точку, из которой ни одна из стен не видна полностью.

В вершинах четырехугольника расположены четыре прожектора, каждый освещает угол в 90 градусов. Докажите, что можно так направить каждый из прожекторов, что вся плоскость окажется освещенной.

У Васи есть пластмассовый угольник (без делений) с углами 30 градусов, 60 градусов и 90 градусов. Ему нужно построить угол в 15 градусов. Как это сделать, не используя других инструментов?

Кролик, готовясь к приходу гостей, повесил в трёх углах своей многоугольной норы по лампочке. Пришедшие к нему Винни-Пух и Пятачок увидели, что не все горшочки с мёдом освещены. Когда они полезли за мёдом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть? (Если да, нарисуйте пример, если нет, обоснуйте ответ.)

Дубликаты не найдены

Колышек в центре ограничивает радиус, верёвка скользящая по другой между двумя колышками - часть круга.

Блин, я недавно здесь. Что делать с правильными ответами на верхушке дерева комментариев? Остальным будет неудобно с ответом на виду

пусть второй способ думают)

Второй способ нашел suse3

Никак - надо было просить какое то время не публиковать ответы :)

Но да ещё второй способ остаётся.

Вообще это не правильное решение, поскольку нужно отчистить полукруг от травы, а не сделать полукруг из травы. Опять же, животное может двигаться не только вперед, но и влево и вправо. В конечном итоге, по условию нет никаких лебедок и регуляторов расстояния, как из веревок и колышков сделать такую систему непонятно. Или я что-то не понял?

Вы не поняли. На рисунке вверху все яно показано, но если вы не поняли. Суть в том, что полукруг - пересечение прямоугольника и круга. Круг мы ограничиваем одним колышком, а прямоугольник ограничиваем конструкцией срава на рисунке. Лебедок никаких нет. Как ограничить прямоугольник? Ставим два колышка на достаточно большом растоянии, прогтягиваем между ними веревку, привязываем к протянутой веревке вторую веревку с помощью петли так, чтобы она свободно ездила по натянутой. Другой конец к козе. Получается не прямоугольник, но он ограничивает полуплоскость.

Так это коза была?!

Две верёвки в разные стороны 10 м и бесконечная

поясни подробнее плиз

Прямая - окружность с бесконечным радиусом. Можно привязать козу к двум колышкам двумя веревками. Расстояние до одного = 10м, до другого 1км (достаточно бесконечно). Поучится полукруг

Фигура ограниченная полуокружностью радиуса 10 м и прямой, которая есть тоже часть окружности бесконечного радиуса

Я что-то не понял совсем

Верно. Ты первый, кто открыл второй способ

если не учитывать еденицы меры, с таким же успехом можно предположить, что если козе завязать рот веревкой - она съест полукруг с нулевым радиусом

Хм, где то я это уже слышал. Там еще было так, ". Добавим собак. Они кусают коз. Но чтобы козы не голодали, собак привязывают. " и нужно удержать козу в полукруге, затем в квадрате или прямоугольнике по моему. Ааа нашел.

"Козы – очень прожорливые животные. Они съедают всю траву, до которой могут дотянуться. Поэтому их держат на привязи.

Привяжите козу на лугу так, чтобы она съела круг.

Какой участок съест коза, если ее привязать между двумя колышками? (Веревка привязана к двум колышкам и продернута сквозь ошейник козы.)

Родион прогуливается по лугу, держа козу на поводке длиной 1м. Его путь имеет вид прямоугольника со сторонами 3 и 5м. Какой участок луга съест коза?

Указание Указание 2 Ответ

Привяжите козу с помощью веревок и колышков так, чтобы она могла съесть траву только внутри участка такой формы:

Натянем на лугу веревку между двумя колышками. У второй веревки привяжем один конец к ошейнику козы, а на втором сделаем петлю, свободно скользящую по веревке. Какой участок выест коза?

Удержите козу с помощью веревок и колышков

в) в прямоугольнике (для прямоугольника решить двумя разными способами).

В следующих задачах участвуют собаки. Они мешают козе есть: коза не ходит туда, куда может добраться собака. Но чтобы козы не остались голодными, собак тоже держат на привязи.

С помощью одной собаки удержите козу

Это шагающий механизм Чебышева. Нужно воссоздать движение его одной ноги. Объяснять и рисовать лень. Ройте гугл сами.

Да, только это работать будет если у тебя палки, а не верёвки.

я бы так решил. Блин, как картинку вставить?

не сработает у вас получится пересечение двух окружностей, а не полукруг

Радиус - x. Ставим колышек - точка А. Привязываем к нему верёвку длиной в x. В на x метров от А. Точка B колышек не ставим. В x метрах от точки B точка C установлена так, чтобы угол CBA был равен 90○. В x метрах от точки В точка D установлена так, что угол BDA был равен 90○, а точка D не равна C . В точках C и D ставим колышки и привязываем верёвку длиной в 2.2x. Привязываем верёвки к козе. И почему ты решил эту задачу только к 9 классу?

Почему длина в 2.2х?

Верно. Я не мог выйти за рамки и понять, что можно привязывать веревку к веревке, тем более скользящую. Есть второй способ. В нем только два колышка и две веревки

Работает безоказно. Правильно

Второй способ нашел suse3

А нарисовать в пэинте для дурачка сможеш

Воткнуть 2 колышка на достаточном расстоянии друг от друга, натянуть между ними веревку. Взять еще одну веревку, один ее конец привязать к козе, а на втором сделать петельку, через которую пропустим самую первую веревку (которая натянута между 2 колышками). Получится, что коза сможет как бы "скользить" по всей длине веревки между колышками. Не знаю, как еще объяснить. Так вот, теперь наша коза может сожрать всю траву, до которой дотянется. На рисунке участок без травы выглядел бы, как сосиска такая. Но мы ее пока не отпускаем)) Теперь второй шаг. Представляем себе эту сосиску, берем ее нижнюю поверхность, находим там середину и вбиваем колышек. Вокруг этого колышка мысленно рисуем окружность. Привязываем к этому колышку козу веревкой, равной радиусу окружности (в данном случае 10). Вуаля, коза сможет слопать всю траву только в ограниченном полукруге (он будет ограничен двумя веревками, привязанными к козе: в то время как одна будет свободна, вторая будет натянута, тем самым ограничивая козу, и наоборот). Объяснила оочень коряво, но уж как смогла)

чтобы ограничить половину круга, строим касательную: 2 колышка на расстоянии друг от друга 10м с пересечением с окружностью посередине, натягиваем веревку. к этой веревке прикрепляем веревку, чтобы она могла "скользить по касательной" длинной 10м и на козу.

Забить колышек в центре круга, привязать к нему козу. Еще один кол забить на кругу и тоже привязать козу. Но веревку использовать подлиннее. Чтоб получился равнобедренный треугольник.

Неверно. Полукруга не будет

Это синоним забора

Готов отвечать на все комментарии по теме

А чего вас заминусили?

Критерии отбора [Есть ответ]

Не дождался ответа от модераторов . Решил выложить на обсуждение Пикабу.
Собственно сама история:

Промучавшись пол дня с задачей ребёнка , решил просить помощи Пикабу

Через пять минут ,по просбе уважаемого (-ой) @Tardak пост был удалён.
Когда Пикабушники спросили причину модератор ответил :

Поэтому хочу повторить вопрос здесь :
Какие критерии полезности и интересности постов используют модераторы?
Может сообщество Пикабу захочет добавить или убрать какие нибудь критерии.

Серия первая. По мотивам матбоя.

1.Существуют ли такие два натуральных числа, наибольший общий делитель которых равен 110, а наименьшее общее кратное равно 2000?

2.Для участников математического боя и членов жюри было приготовлено конфет столько же, сколько булочек и стаканов чая вместе. Каждый школьник съел по конфете и выпил по стакану чая, после чего осталось стаканов чая и конфет вместе столько, сколько булочек. Найдется ли стакан чая для заглянувшего к ним члена жюри?

3.Мимо наблюдателя по дороге Кострома - Иваново проехали с равными между собой промежутками времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками, но в другом порядке: автобус, автомобиль, мотоцикл. Найдите скорость автобуса, если скорость автомобиля 60 км/ч, а мотоцикла - 30 км/ч.

4.Незнайка отметил на плоскости 15 точек и утверждает, что какое бы натуральное число от 1 до 7 ему не назвали, он может указать прямую, на которой лежит ровно столько отмеченных точек. Прав ли он?

5.На витрине ювелирного магазина лежат 9 золотых монет весом 100г, 101г, . 108г. Рядом с каждой монетой лежала этикетка, указывающая вес монеты. Первого апреля шутник переложил этикетки. Продавец точно знает, какая монета сколько весит. За какое наименьшее число взвешиваний на чашечных весах со стрелкой, показывающей разность весов на чашках, он сможет показать хозяину, который не знает, какая монета сколько весит, как правильно положить этикетки?

6.Фунтик-Шпунтик развлекается тем, что выписывает все натуральные числа, цифры которых убывают, а затем в каждом вставляет знаки сложения и вычитания между соседними цифрами по порядку “–”, “+”, “–”, “+”, . и считает результат. (Например, 97641 превращается в 9–7+6–4+1=5.) В конце он все результаты сложил. Какое число получено?

Серия 4. Очень-очень маленькая.

1.Таня стоит на берегу речки. У неё есть два глиняных кувшина: один – на 5 литров, а про второй Таня помнит лишь то, что он вмещает то ли 3, то ли 4 литра. Помогите Тане определить ёмкость второго кувшина.

2. В каждой клетке бесконечного клетчатого поля написано по натуральному числу. Докажите, что найдется число, не превосходящее всех своих соседей.

3.На рисунке показана схема расположения тропинок и полянок (A, B, C, D, E и F) в Дремучем лесу. а)Сколько существует способов попасть с полянки А на полянку F, побывав на полянках B, С, D и Е по одному разу?
б) Жители Дремучего леса собрались протоптать еще одну тропинку так, чтобы способов стало 132. Между какими полянками следует протоптать эту тропинку?

4.На доске размером 9×9 клеток закрашены в черный цвет первый, третий, пятый, седьмой и девятый столбцы. Вася хочет расположить на этой доске Т-тетраминошку. Каких способово у него больше: тех, в которых в фигурке окажется 3 черных клетки, или тех, в которых одна?

Серия 6. О голодной козе.

Козы прожорливы и съедают все, до чего могут дотянуться. Поэтому коз держат на привязи.

1.Нарисуйте участок луга, который выест коза, привязанная двумя веревками длиной 2 м каждая к двум одиноко стоящим колышкам, находящимся друг от друга на расстоянии: а) 2 метра; б) 4 метра.

2. Привязывать козу можно либо к колышкам, либо к горизонтальной палке. Как привязать с помощью веревок козу так, чтобы она съела всю траву на участке в форме:
а) полукруга;
б) сектора;
в) прямоугольника;
г) фигуры, изображенной на рисунке 2;
д) фигуры, изображенной на рисунке 3;
е) правильного треугольника;
ж) правильного шестиугольника.

3. Коза привязана к одиноко стоящему на лугу колышку. Введём дополнительно в действие собаку, которую будем привязывать к колышкам или к горизонтальным палкам, и она будет мешать козе есть. Как этой собакой удержать козу:
а) в кольце?
б) в полукруге?
в) в фигуре, изображенной на рис.4?
г) в фигуре, изображенной на рис.5?

4.Удержите непривязанную козу с помощью одной собаки в треугольнике.

5.а) Один конец шеста длиной 4 метра прикреплен к столбу и свободно вокруг него вращается. К другому концу шеста веревкой длиной 1 метр привязана коза. Какую фигуру выест коза? А если веревка имеет длину 5 метров?
б) А если веревку заменить шестом соответствующей длины?

Серия 8. Зато с картинкой.

1.Три коржика тяжелее пяти пирожков. Могут ли семь коржиков быть легче тринадцати пирожков?

2.Можно ли придумать пять таких слов, чтобы каждое имело хотя бы одну общую букву ровно с тремя другими.

3. Из Манчестера в Ливерпуль ведут два шоссе с односторонним движением, пересеченные десятью проселками (см. рис.). Машина выезжает из М в Л по одному из шоссе и, доезжая до любой развилки, может либо свернуть на проселок, либо не сворачивать. Свернув, она проезжает проселок до конца и продолжает путь по другому шоссе (по тем же правилам). Сколькими разными способами можно проехать из Манчестера в Ливерпуль?

4.Математическая черепаха сидит в левом нижнем углу прямоугольника 3´n. Докажите, что количество способов добраться до правой верхней клетки равно количеству способов записать в строчку 2 единицы и n–1 нуль.

5.Фокусник кладет перед зрителем колоду из n карт, и просит его посмотреть и запомнить одну карту. После этого фокусник раскладывает все карты в 6 стопок, и просит зрителя сказать, в какой из них лежит загаданная карта. Затем фокусник тасует карты, опять раскладывает их в 6 стопок, и просит зрителя назвать ту из стопок, в которой на этот раз лежит задуманная карта. Едва услышав ответ, фокусник сразу вытаскивает загаданную карту из стопки. Для какого наибольшего n можно с успехом показывать такой фокус?

6.Какое наибольшее количество натуральных чисел, не превышающих 100, можно выбрать так, чтобы ни одно из них не делилось на другое?

7.Даша и Саша играют в игру. Саша выбирает число n и на доске магическим образом появляются числа от 1 до n. За это Саша уступает Даше первый ход. За один ход разрешается вычеркнуть любое число вместе со всеми его делителями. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Серия 10. Двузначная

1. Четыре страны имеют форму треугольников. Нарисуйте, как могли быть расположены друг относительно друга страны, если у каждой из них есть общие границы (по отрезку) с тремя другими.

2. Двое мальчиков катались на лодке. К берегу подошел отряд солдат. Лодка так мала, что на ней могли переправиться двое мальчиков или только один солдат. Смогут ли солдаты переправиться через реку?

3. Серый Волк позвонил на Бейкер-стрит и заявил, что у него украли очень ценную вставную челюсть, инкрустированную бриллиантами. Подозреваемые — Ниф-Ниф, Наф-Наф и Нуф-Нуф. Известно, что:

а)каждый из троих подозреваемых в день кражи побывал в гостях у волка, и никто больше к нему не заходил;

б) если Ниф-Ниф виновен, то у него был ровно один сообщник;

в)если Нуф-Нуф не виновен, то не виновен также и Наф-Наф;

г) если Наф-Наф не виновен, то не виновен также и Нуф-Нуф;

д) если виновны двое, то Ниф-Ниф один из них.

Кому Шерлок Холмс предъявит обвинение?

4. Длину прямоугольника уменьшили на 10%, а ширину уменьшили на 20%. При этом периметр прямоугольника уменьшился на 12%. На сколько процентов уменьшится периметр прямоугольника, если его длину уменьшить на 20%, а ширину уменьшить на 10%?

5. В припортовой таверне пираты Боб и Иван состязались в изготовлении и употреблении крепких напитков. Боб изготовил коктейль из рома и виски, а Иван смешал водку с портвейном. Известно, что ром крепче водки, а виски крепче портвейна. Может ли смесь Ивана оказаться крепче коктейля Боба?

6. Сколькими способами можно выбрать из чисел от 1 до 100 три числа так, чтобы их сумма делилась на 3?

7. Играют трое. На столе лежат 2010 кучек конфет, по 100 штук в каждой. За ход разрешается взять произвольное количество конфет из одной кучи. Ходы делаются по очереди: Даша – Соня – Юля – Даша – Соня – Юля и т.д. Проигрывает тот, кто не может сделать ход. Могут ли Соня и Юля, объединившись, довести Дашу до проигрыша?

Серия 12. Зверинец.

1.
Доктор Айболит раздал четырём заболевшим 1234 чудодейственные таблетки. Кощей получил на одну таблетку больше, чем кикимора, Баба Яга на одну больше, чем Кощей, а Змей Горыныч – на одну больше, чем Баба Яга. Сколько таблеток придётся съесть Змею Горынычу?

2. Расшифруйте ребус: Б + БЕЕЕ = МУУУ

3. В квадратном ковре со стороной 1 м моль проела 51 точечную дырку. Докажите, что некоторой квадратной заплаткой стороной 20 см можно закрыть не менее трёх дырок.

4. На бесконечной в обе стороны клетчатой ленте сидит кузнечик, который умеет прыгать на 7 клеток вправо и на 4 клетки влево. Докажите, что он сможет добраться до любой клетки.

5. Однажды профессор консерватории пригласил к себе в гости музыкантов Мартышку, Козла, Осла и Косолапого Мишку. В комнате у профессора вокруг стола стоит несколько стульев. Профессор насчитал 120 способов рассадить на них своих гостей. После этого он решил подсчитать, в скольких способах Мартышка и Мишка сидят на соседних стульях, и насчитал 60 способов. Потом он решил подсчитать, а в скольких способах Козел и Осел не сидят рядом. И насчитал 40 способов. Докажите, что профессор где-то ошибся.

6. Перед Белкой шоколадка размера а) 8×8 б) 5×6 долек. В одной из долек спрятан орех. Белка может указать на любую прямоугольную часть и узнать, находится ли в ней орех. Какого наименьшего количества вопросов ей хватит, чтобы найти орех?

7. На клетчатой бумаге отметили 100 клеток. Докажите, что из них можно выбрать 50 так, чтобы среди выбранных клеток не было соседних по стороне.

Серия 13, начало.

а) Докажите это с помощью индукции.

б) Докажите это с помощью геометрии.

2. В конференции участвовали 19 ученых. После конференции каждый из них отправил 2 или 4 письма участникам этой конференции. Могло ли получиться так, что каждый участник получил по 3 письма?

3. Количество интегралов, взятых Марией Михайловной, выражается трехзначным числом, начинающимся на 9. Если первую цифру этого числа перенести в конец, то получим количество интегралов, взятых Анной Михайловной. Известно, что Анна Михайловна взяла на 90 интегралов меньше. Выразите их мучения численно.

Серия 13, продолжение.

На какое минимальное количество прямоугольников можно разрезать следующую фигуру:
Правильный треугольник разбит прямыми, параллельными сторонам, на 9 равных правильных треугольников. Петя отметил один из входящих в него треугольников невидимыми чернилами. Вася может указать любой треугольник со сторонами, идущими по линиям разбиения, и Петя скажет ему, лежит ли отмеченный треугольник в указанном. За какое наименьшее число таких вопросов Вася наверняка сможет найти отмеченный треугольник?
Вражеская шпионская сеть устроена следующим образом. Каждый из шпионов знает ровно четырех других. Получив какую-либо информацию шпион передает ее всем другим, известным ему, шпионам. Однажды, при передаче одного важного сообщения все шпионы сработали безукоризненно, кроме Васи, который не смог связаться со своим знакомым шпионом Петей. Докажите, что, несмотря на это вся сеть будет оповещена.
Все рыцари и лжецы острова построились по кругу, и каждый сказал, про соседа справа – рыцарь он или лжец. На основании этой информации, путешественник смог сообразить, какова доля рыцарей в населении. А чему она равна?

Серия 14. Жужжащая.

1. Максим должен был разделить число на 2, а к результату прибавить 3, а он, по ошибке, умножил число на 2, а от полученного произведения отнял 3. Ответ все равно получился правильный. Какой?

2. Артем и Саша вместе знают столько же плохих слов, сколько Игорь и Дима. А Артем с Димой знают таких слов больше, чем Саша с Игорем. Расположите юных лингвистов по количеству известных им плохих слов, если известно, что Саша знает их больше, чем Артем и Игорь вместе взятые.

3. В квадратном ковре со стороной 1 м моль проела 15 точечных дырок. Докажите, что из него можно вырезать неповрежденный круг радиуса 12,5 см.

4. На шестиугольной решетке (см. рисунок) пчёлы сложили мед в 300 шестиугольников. Докажите, что из них можно выбрать 100 так, чтобы не было соседних по стороне.

5. Выразите без многоточий число 1+2+4+…+2 100 .

6. На клетчатой бумаге построены несколько прямоугольников со сторонами, параллельными линиям сетки и общим центром О в одном из узлов сетки. За один вопрос можно про любой из узлов узнать, у скольких прямоугольников он лежит внутри. Как за четыре вопроса узнать, сколько прямоугольников содержат только один узел О?

7. Есть n одинаковых банок. Из них n-1 доверху заполнены красками разных цветов, а последняя пустая. Разрешается переливать из любой банки в любую произвольное количество краски. Докажите, что можно сделать так что каждая из n банок будут заполнены поровну равномерной смесью всех красок.

Олипиада ЮМШ 6 класса 5. Есть доска 9×9 клеток. В каждую клетку поставили число 0, 1 или 2 так, чтобы в каждом квадратике 2×2 сумма была больше четырёх. Докажите, что сумма всех чисел на доске не меньше 89.6. Мама выдала Ванечке двузначное число. Ванечка сложил в столбик это число с ним же, после чего проделал то же самое с полученным результатом, и так 11 раз. Когда мама стала проверять его вычисления, выяснилось, что Ванечка при сложении двойки с двойкой получал всегда вместо четырёх пять (или шесть, если там был ещё перенос). В итоге у него получилось число, которое оканчивается ровно на один ноль. Каким могло быть исходное число?7. Круг разбит на 100 секторов. Мирза и Егор по очереди заполняют сектора (в произвольном порядке) натуральными числами (первым ходит Мирза). Когда все сектора заполнены, Мирза пишет на доску ещё одно натуральное число, после чего Егор режет круг на две половинки (по 50 секторов). Если сумма чисел в одной из них оканчивается на те же две цифры, что и число на доске, то побеждает Егор, иначе побеждает Мирза. Кто победит при правильной игре?

15 серия: Начало.

1.
Диана, Кирилл и Афанасий задумали по трехзначному числу. Могло ли так оказаться, что сумма числа Афанасия с числом Дианы равна 600, а сумма числа Кирилла с числом Дианы равна 1500?

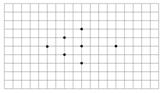
2. На клетчатой бумаге поставлено 7 точек так, как показано на рисунке. Перечеркните все эти точки тремя отрезками, не отрывая карандаша от бумаги. Отрезки не обязательно должны проходить по линиям сетки.

3. На математический кружок пришли три длинноволосых ребёнка. Их фамилии - Кубанец, Чиковани и Никитина, имена - Саша, Женя и Дима. Учитель знает об этом, но на взгляд не может определить, кто из них мальчик, а кто девочка. Каждый из детей назвал своё имя и фамилию, причём учителю известно, что мальчики называют и то и другое неверно, а девочки правильно. Может ли учитель гарантированно определить по ответам детей, сколько среди них мальчиков? (Кубанец и Чиковани могут быть как мальчиками, так и девочками, Саша и Женя тоже).

4. В куче лежит N камней, N>3. Двое играют в игру. Первый игрок забирает из кучи один камень. Каждым следующим ходом можно забрать либо ровно на один камень больше, либо ровно на один меньше, чем только что взял соперник, но не менее одного камня. Проигрывает тот, кто не может сделать очередной ход. Кто из игроков может выиграть, как бы ни играл его соперник?

Серия первая. По мотивам матбоя.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Читайте также: