Как обойти конем всю шахматную доску

Опубликовано: 26.04.2024

Эта глава посвящена самой интересной задаче о коне и, пожалуй, вообще самой известной шахматно-математической задаче. Она заключается в нахождении маршрута коня на шахматной доске.

Обойти конем все поля шахматной доски, посетив каждое из них по одному разу.

В литературе эту задачу обычно называют просто задачей о ходе коня. Особая популярность задачи объясняется тем, что в XVIII и XIX вв. ею занимались многие крупные математики, в том числе великий Леонард Эйлер, посвятивший ей большой мемуар «Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию»21. Хотя задача была известна и до Эйлера, лишь он впервые обратил внимание на ее математическую сущность, поэтому задачу часто связывают с его именем.

Значительно труднее проблема, состоящая не в отыскании определенного маршрута коня, а в нахождении всех маршрутов и подсчете их числа. Увы, эта задача не решена до сих пор, и шансов на успех немного. Известно, правда, что число решений не превосходит C 63 168 (это число состоит из ста цифр), но больше 30 миллионов. Математик Ф. Миндинг, подошедший к проблеме с алгебраической точки зрения, предложил метод, позволяющий вывести формулу для числа всех решений, однако вычисления, которые следует при этом произвести, практически неосуществимы, и поэтому метод Миндинга представляет лишь теоретический интерес.

Литература, посвященная задаче о ходе коня, весьма обширна. Те или иные методы нахождения маршрутов можно найти в самых разнообразных источниках. Среди них следует выделить книгу Крайчика «Проблема коня», которая, как видно из названия, целиком посвящена этой теме (эта книга входит в упомянутую во введении фундаментальную работу Крайчика). Об алгебраическом подходе, основанном на исследованиях Яниша_д рассказывается у Окунева, а у Шуберта22 можно найти подробный исторический обзор задачи о ходе коня. Остановимся на некоторых наиболее интересных методах нахождения маршрутов коня.

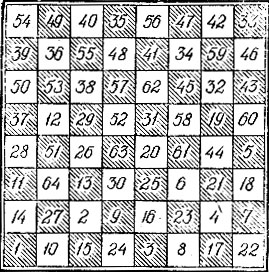
Рамочный метод Мунка и Коллини. (Коллини - секретарь знаменитого философа Вольтера). Шахматную доску разделим па две части: внутреннюю, состоящую из 16 полей, и внешнюю, имеющую форму рамы и состоящую из 48 полей (рис. 23,а). На полях внутреннего квадрата запишем заглавные буквы А, В, С, D - так, чтобы каждая из них, повторенная четыре раза, образовала квадрат или ромб, по всем сторонам которого может ходить конь. Те же буквы, только строчные, запишем на рамочных полях так, чтобы ходы коня по каждой из букв образовали замкнутые многоугольники, окаймляющие центральный квадрат.

Конь начинает ходить от какого-нибудь рамочного поля, проходит вокруг рамы по выбранной букве, например а, и в 12 ходов исчерпывает эту букву (при этом последнее поле не должно быть угловым). Затем он переходит во внутренний квадрат, но не на букву Л, а на какую-нибудь другую - В, С или D. Пройдя все поля, обозначенные этой буквой, конь снова переходит на раму - на букву, по которой еще не ходил, и вновь обегает вокруг рамы, исчерпывая до конца эту букву, - и т. д., пока не пройдет по всей доске.

Метод Полиньяка и Роже - деление на четверти. Этот метод проще предыдущего, хотя и похож на него. Разделим доску крестом на четыре квадрата (рис. 23,б). В каждом из них расставим буквы а, b, с, d точно так же, как во внутреннем квадрате на рис. 23,а. Конь начинает движение с любой буквы, проходит в выбранном квадрате по всем четырем полям с этой буквой, затем переходит на ту же букву соседнего квадрата, и т. д. Исчерпав все 16 полей с одной буквой, он меняет ее и снова зигзагом обегает доску. После четырех таких кругов все поля будут пройдены (как и в предыдущем методе, «круговые» маневры не должны заканчиваться на угловом поле).

Маршруты и пути коня по доске удобно нумеровать последовательными числами 1, 2, 3 … в соответствии с порядком ходов. В полном маршруте коня начальное поле имеет номер 1, а конечное - 64. Разумеется, изменив направление данного маршрута на противоположное, мы всегда можем начальное поле сделать конечным, и наоборот. Если маршрут замкнут, то поля 1 и 64 связаны ходом коня.

Метод Эйлера и Вандермонда. Этот метод, хотя и не является таким простым и эффектным, как два предыдущих, позволяет, в отличие от них, получать самые разнообразные маршруты коня.

В основе метода лежит возможность замены обратными всех ходов, начиная с поля, связанного ходом коня с конечным.

В качестве примера рассмотрим маршрут на рисунке 24, а. Используя связь поля 31 с конечным полем 64, мы можем получить еще один маршрут. Оставим все числа 1, …, 31 на своих местах, а числа 32, 33, …, 64 заменим соответственно числами 64, 63, …, 32. Иначе говоря, один последовательный путь (от поля 32 до поля 64) мы заменили другим, обратным (от 64 до 32). Теперь поле b4, поменявшее номер 32 на 64, стало конечным. Новый маршрут в старой нумерации полей можно записать так: от 1 до 31, 31 - 64 (один ход - с поля 31 на 64), от 64 до 32.

Указанный прием можно повторять многократно, получая все новые и новые маршруты. В исходном маршруте поле 49 также связано с 64, что дает нам другой производный маршрут: от 1 до 49, 49 - 64, от 64 до 50. В первом из найденных маршрутов поле 32 связано с 43 - и мы можем получить второй производный маршрут: от 1 до 31, 31 - 64, от 64 до 43, 43 - 32, от 32 до 42, и т. д.

Если дан некоторый маршрут, то, проявив определенную изобретательность, его можно преобразовать так, чтобы любое наперед заданное поле стало конечным (а эначит, и начальным). Пусть, например, мы хотим сделать конечным поле d4, имеющее номер 56. Свяжем его с полем 64 такими ходами: 64 - 31 - 32 - 57 - 56. Теперь дважды преобразуем исходный маршрут коня (рис. 24,а): 1) от 1 до 31, 31 - 64, от 64 до 32; 2) от 1 до 31, 31 - 64, от 64 до 57, 57 - 32, от 32 до 56. Последний маршрут заканчивается на поле d4, к чему мы и стремились. Описанным методом из незамкнутого маршрута иногда удается получить замкнутый. Так, для превращения маршрута на рис. 24,а в замкнутый достаточно пути: от 11 до 17, от 10 до 1, от 18 до 31, от 64 до 57, от 32 до 45, от 56 до 46 заменить соответственно такими: от 1 до 7, от 8 до 17, от 18 до 31, от 32 до 39, от 40 до 53, от 54 до 64.

Основное достоинство метода Эйлера и Вандермонда заключается в том, что он помогает нам завершить путь коня в тех случаях, когда мы двигались без всякой системы и попали в тупик - дальше идти некуда, а еще остались непройденные поля. Пусть, например, мы уже побывали на 62 полях доски (путь от 1 до 62 на рис. 24,б, а поля а и b не посетили). Здесь поле а связано с полем 10, а поле 62 с полем 9. Это позволяет нам преобразовать путь от 1 до 62 в следующий: от 1 до 9, 9 - 62, от 62 до 10. После перенумерации поле b2 в этом пути меняет номер 10 на 62 и под номером 63 к пути присоединяется поле а. Теперь нам осталось присоединить к пути поле b. В этом нам помогает то обстоятельство, что из двух последовательных полей 57 и 58 первое связано с полем b, а второе - с полем а (имеющим сейчас номер 63). Теперь наш путь (в исходной нумерации) превращается в такой: от 1 до 9, 9 - 62, от 62 до 58, 58 - а, а - 10, 10 - 57. После очередной перенумерации номер 63 теперь получает бывшее поле 57, и, присоединяя к нему поле b, получаем, наконец, искомый маршрут (рис. 24,а; нумерация здесь последовательная - от 1 до 64).

Рассмотренные нами преобразования - далеко не единственные, позволяющие получать из одних маршрутов другие. Упомянем еще преобразования, связанные с поворотами доски и отражениями ее относительно осей симметрии или центра симметрии. Различные свойства маршрутов, основанные на идеях симметрии, исследованы в указанной ранее литературе. Заметим, кстати, что из одного замкнутого маршрута коня можно получить сразу 127 новых: 63 - сдвигом нумерации ходов, а из полученных 64 - еще столько же изменением направления маршрута.

Правило Варнсдорфа. Это довольно эффективное правило заключается в следующем.

1) при обходе доски коня следует всякий раз ставить на поле, из которого он может сделать наименьшее число ходов на еще не пройденные поля; 2) если таких полей несколько, то разрешается выбирать любое из них.

Правило Варнсдорфа предложено более 150 лет назад. Долгое время считалось, что оно действует безукоризненно. Позднее было установлено, что его вторая часть не совсем точна. Если в распоряжении коня имеется несколько возможностей, упомянутых в первой части правила, то не все они являются равноценными. Полную яспость в этот вопрос удалось внести при помощи ЭВМ. Машинный эксперимент, проведенный в Тульском пединституте под руководством А. Есаяна, показал, что с какого бы поля доски конь ни начал свой маршрут, можно так пользоваться второй частью правила Варнсдорфа, что он попадет в тупик раньше, чем посетит все поля доски.

Анимация прохождения коня через все клетки поля шахматной доски 5 x 5

Задача о ходе коня — задача о нахождении маршрута шахматного коня, проходящего через все поля доски по одному разу.

Эта задача известна по крайней мере с XVIII века. Леонард Эйлер посвятил ей большую работу «Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию» (Шаблон:Нет АИ 2). В письме к Гольдбаху он сообщал: Шаблон:Цитата

Содержание

1 Формулировка задачи
2 Методы решения
- 2.1 Метод Эйлера
- 2.2 Метод Вандермонда
- 2.3 Правило Варнсдорфа
3 Примечательные маршруты
- 3.1 Маршрут Яниша
- 3.2 Маршрут, найденный шахматным автоматом
- 3.3 Мнемоническое стихотворение
4 Обобщение на произвольные доски
- 4.1 Замкнутые маршруты
- 4.2 Незамкнутые маршруты
5 См. также
6 Примечания
7 Ссылки

Формулировка задачи [ править | править код ]

Граф, соответствующий шахматной доске 8×8. Указанные степени вершин показывают количество различных ходов коня из соответствующих полей доски.

В терминах теории графов каждый маршрут коня, проходящий через все поля шахматной доски, соответствует гамильтонову пути (или циклу, если маршрут замкнутый) в графе, вершинами которого являются поля доски, и два поля соединены ребром, если с одного можно попасть на другое за один ход коня.

Количество всех замкнутых маршрутов коня (гамильтоновых циклов) без учёта направления обхода равно 13 267 364 410 532 [1] .

Количество всех незамкнутых маршрутов (с учётом направления обхода) равно 19 591 828 170 979 904.

Методы решения [ править | править код ]

Метод Эйлера [ править | править код ]

Метод Эйлера состоит в том, что сначала конь двигается по произвольному маршруту, пока не исчерпает все возможные ходы. Затем оставшиеся непройденными клетки добавляются в сделанный маршрут, после специальной перестановки его элементов.

Рассмотрим в качестве примера следующий маршрут:

55	58	29	40	27	44	19	22
60	39	56	43	30	21	26	45
57	54	59	28	41	18	23	20
38	51	42	31	8	25	46	17
53	32	37	a	47	16	9	24
50	3	52	33	36	7	12	15
1	34	5	48	b	14	c	10
4	49	2	35	6	11	d	13

Сначала попытаемся из незамкнутого маршрута сделать замкнутый. Для этого рассмотрим, куда можно пойти с полей 1 и 60. С поля 1 можно пойти на поля 2, 32 и 52, а с 60 - на 29, 51 и 59. В этих двух наборах есть поля, различающиеся на единицу, а именно - 51 и 52. Благодаря этому можно сделать маршрут замкнутым, обратив его часть. Для этого перенумеруем поля с 52 по 60 в обратном порядке. После этого у нас получается замкнутый маршрут:

57	54	29	40	27	44	19	22
52	39	56	43	30	21	26	45
55	58	53	28	41	18	23	20
38	51	42	31	8	25	46	17
59	32	37	a	47	16	9	24
50	3	60	33	36	7	12	15
1	34	5	48	b	14	c	10
4	49	2	35	6	11	d	13

Теперь можно включить в маршрут некоторые из непройденных клеток. Так как наш маршрут замкнутый, то его можно разорвать в произвольном месте и к одному из концов прицепить подходящую цепочку из непройденных клеток. Например, если разорвать цепочку в клетке 51 (перенумеровав клетки и сделав её последней, а 52 - первой), то сможем удлинить нашу цепочку на клетки a, b и d, которые станут клетками 61, 62 и 63.

Метод Вандермонда [ править | править код ]

Вандермонд попытался свести задачу к арифметической. Для этого он обозначал маршрут коня по доске в виде последовательности дробей $<\displaystyle <\frac <x><y>>>$
, где x и y — координаты поля на доске. Очевидно, что в последовательности дробей, соответствующей ходам коня, разность числителей двух соседних дробей может быть только 1 или 2, при том, что разность их знаменателей составляет соответственно 2 или 1. Кроме того, числитель и знаменатель не могут быть меньше 1 и больше 8.

Его метод нахождения подходящей последовательности аналогичен методу Эйлера, но позволяет находить маршруты коня только для досок чётной размерности.

Правило Варнсдорфа [ править | править код ]

Правило Варнсдорфа, являющееся разновидностью жадного алгоритма для отыскания маршрута коня, формулируется так:

При обходе доски конь следует на то поле, с которого можно пойти на минимальное число ещё не пройденных полей. Если таких полей несколько, то можно пойти на любое из них.

Долгое время считалось, что правило Варнсдорфа работает безукоризненно. Позднее с помощью компьютеров была установлена неточность во второй его части: если существует несколько подходящих полей, то не все они равноценны, и произвольный выбор поля может завести коня в тупик. На практике однако вероятность попадания в тупик невелика даже при вольном пользовании второй частью правила Варнсдорфа. [2]

Примечательные маршруты [ править | править код ]

Маршрут Яниша [ править | править код ]

50	11	24	63	14	37	26	35
23	62	51	12	25	34	15	38
10	49	64	21	40	13	36	27
61	22	9	52	33	28	39	16
48	7	60	1	20	41	54	29
59	4	45	8	53	32	17	42
6	47	2	57	44	19	30	55
3	58	5	46	31	56	43	18

Маршрут коня, найденный К. Я. Янишем, образует полумагический квадрат, а при повороте доски на 180° первая половина маршрута (номера с 1 до 32) переходит во вторую (номера с 33 по 64).

Маршрут, найденный шахматным автоматом [ править | править код ]

Шахматный автомат нашёл замкнутый маршрут коня, изображенный на диаграмме справа.

Мнемоническое стихотворение [ править | править код ]

Обойти конём все шахматные клетки по одному разу, к тому же сделать это «вслепую», начав или закончив на любой клетке по желанию «зрителя», можно следуя стихотворению: [3]

Алеет Осень Ценными Дарами,
Еще Один Животворящий День.
Хлеба Червонят Желтыми Шнурами,
Хрустальных Вод Философична Сень.

Два Вечера Цеплявшиеся Шишки
Артист Писал, Бездонна Синева.
Дорожный Шлак Целуют Червячишки,
Еще Покрыта Флоксами Трава.

Дымится Чай Эффектней Шоколада,
Фарфоры Чашек Достаются Трем,
Блондинке Девушка Дана Отрада
Форшмак Делить Холодным Острием.

Жена, Толкая Хилую Подругу,
Желает Сняться Этим Выходным,
Ценя Сама Арктическую Вьюгу,
Бросает Шар Арбуза Четверым.

Цикад Пяток, Едва Чревовещая,
Дарует Дрему Фикусам Окна.
Хотя Довольны Жаждавшие Чая,
Хозяин Шумно Жертвует Вина.

Фокстротами Шесть Девушек Пленились,
Эстрадных Танцев Фантастичней Па,
Едва Ступающий Цыпленок Вылез,
А Селезень Блуждающий Пропал.

Алеет Тело Бронзовой Осины,
Царит Теней Ажурная Длина.
Беззвучней, Чем Автомобиля Шины,
Болоту Ветер Дарит Семена.

Фонарь Восьмью Химерами Сияет,
Жук Прилетает, Хлопая, Туда.
Желанна Осень, Если Довершает
Ценнейший Отдых Бодрого Труда.

Первые буквы задают координаты ходов:

Алеет Осень = А1; Ценными Дарами = С2; и т. д.

В каждую строфу вставлена подсказка, помогающая не перепутать последовательность строф: ещё ОДИН, ДВА вечера, достаются ТРЁМ и т.д.

Обобщение на произвольные доски [ править | править код ]

Замкнутые маршруты [ править | править код ]

Количество замкнутых маршрутов с учётом направления в два раза больше. Замкнутые маршруты существуют на досках $<\displaystyle n\times n>$
для всех чётных " width="" height="" />
(Шаблон:OEIS).

Незамкнутые маршруты [ править | править код ]

Для неквадратных досок незамкнутый обход конём существует только при выполнении следующих условий: если одна сторона доски равна 3, то другая должна быть либо 4, либо не меньше 7; если же обе стороны больше 3, то обход коня возможен на всех досках, кроме 4×4. В частности, незамкнутые маршруты существуют на квадратных досках $<\displaystyle n\times n>$
для всех $<\displaystyle n\geqslant 5>$
. [4] Количество незамкнутых маршрутов на досках $<\displaystyle n\times n>$
образуют Шаблон:OEIS.

Мы встречались уже в этом разделе с вопросом, может ли конь обойти часть шахматной доски, побывав при этом на каждом поле только один раз.

Вот еще одна старинная задача о ходе шахматного коня:

Требуется обойти конем все 64 клетки шахматной доски так, чтобы на каждой клетке конь был только один раз и затем возвратился бы в клетку, из которой вышел.

Задачей этой занимался Эйлер и в письме к Гольдбаху (26 апреля 1757 года) дал одно из решений ее. Вот что, между прочим, пишет он в этом интересном письме:

". Воспоминание о предложенной когда-то мне задаче послужило для меня недавно поводом к некоторым тонким изысканиям, в которых обыкновенный анализ, как кажется, не имеет никакого применения. Вопрос состоит в следующем. Требуется обойти шахматным конем все 64 клетки шахматной доски так, чтобы на каждой клетке он побывал только один раз. С этой целью все места, которые занимал конь при своих последовательных ходах, закрывались марками. Но к этому присоединилось еще требование, чтобы начало хода делалось с данного места. Это последнее условие казалось мне очень затрудняющим вопрос, так как я скоро нашел некоторые пути, при которых, однако, выбор начала для меня свободен. Я утверждаю, однако, что если полный обход коня будет возвратный, т. е. если конь из последнего места опять может перейти на первое, то устраняется и это затруднение. После некоторых изысканий по этому поводу я нашел, наконец, ясный способ находить сколько угодно подобных решений (число их, однако, не бесконечно), не делая проб. Подобное решение представлено на рисунке (рис. 153).

Рис. 153

Конь ходит в порядке, указанном числами. Так как из последнего места 64 он может перейти на 1, то этот полный ход есть возвратный".

Таково решение задачи о ходе шахматного коня, данное Эйлером. В письме не указаны ни приемы, ни путь, которыми знаменитый ученый пришел к своему открытию. Сейчас мы укажем на методы иных, более симметричных и методичных решений.

Разделим шахматную доску на две части: внутреннюю, состоящую из 16 клеток, и краевую (рис. 154).

Рис. 154

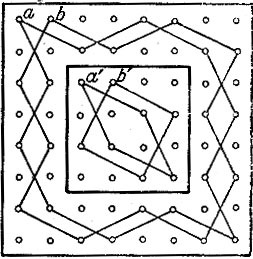
Каждые 12 клеток краевой доски, обозначенные у нас Одинаковыми буквами, дают один из частных зигзагообразных путей шахматного коня вокруг доски; точно так же четыре одноименные клетки внутренней части доски дают частный замкнутый путь шахматного коня в виде квадрата или в виде ромба. Рис. 155 представляет два зигзагообразных частных пути коня на краевой части доски. Эти пути обозначим буквами а и b. Там же начерчены и два пути на внутренней части доски. Эти пути назовем a' и b' соответственно обозначениям на рис. 154.

Рис. 155

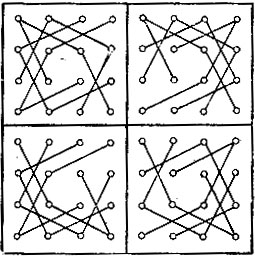
Закончив какой-нибудь частный круговой путь по краевой части доски, конь может перескочить на любой из трех путей другого наименования на внутренней части доски. Нетрудно (стоит лишь взять в руки шахматную доску и коня) найти, и притом различными способами, четыре пути из 16 клеток - таких, например, как

В самом деле, всмотритесь в рис. 154 и 155 или поставьте перед собой шахматную доску, и вы увидите, что для получения частного пути коня в 16 клеток надо только краевой частный круговой путь из 12 клеток соединить с внутренним путем, но другого наименования, прямой чертой, уничтожая при этом в каждом из частных круговых путей замыкающую линию. Так получим четыре частных круговых пути по 16 клеток. Эти четыре частных . пути по 16 клеток опять можно соединить различным образом и получить полный путь шахматного коня из 64 клеток.

Итак, ставят коня на какую-нибудь клетку, например, краевой части доски и описывают по ней путь из 12 клеток; вслед за тем конь перепрыгивает на клетку одного из трех (не одноименных) внутренних путей, проходит этот путь в любом направлении и перескакивает опять на краевую часть, где снова делает следующий частный зигзагообразный путь из 12 клеток, вновь перескакивает на один из внутренних, не одноименных с предыдущим, путей, описывает его, переходит опять на новый краевой путь и т. д., пока не обойдет все 64 клетки.

Способ решения задачи настолько прост и легок, что не нуждается в более подробных разъяснениях и указаниях.

Можно эту же задачу решить и другим, не менее легким, приемом. Здесь для удобства доска делится на 4 части по 16 клеток в каждой двумя серединными линиями (рис. 156) 16 клеток каждой четверти, обозначенных одинаковыми буквами, можно соединить посредством сторон двух квадратов и двух ромбов, не имеющих ни одной общей вершины (рис. 157). Соединяя, в свою очередь, одноименные квадраты и ромбы всех четвертей доски, можно получить четыре частных круговых возвратных пути из 16 клеток. Соединяя затем эти последние пути, получим полный путь коня в 64 клетки.

Рис. 156

Рис. 157

Полезно сделать еще следующие замечания. На каждой четверти доски ромбами и квадратами обозначены по четыре пути коня. Если соединим ромбы и квадраты, обозначенные одинаковыми буквами во всех четырех четвертях доски, получим по четыре частных возвратных пути из 16 клеток.

Некоторые трудности могут представиться кому-нибудь, когда для получения полного пути в 64 клетки он начинает соединять между собой эти четыре частных пути по 16 клеток. Здесь полезно иметь в виду, что цепь (или ряд ходов) можно видоизменять, не разрывая ее. Основано это на так называемом правиле Бертрана, которое состоит в следующем.

Пусть имеем незамкнутую цепь ходов, проходящих через клетки A, B, С, D, E, F, G, H, I, J, К, L и пусть оконечности этой цепи будут А и L. Если клетка, например D, отличная от предпоследней K, находится от последней L на расстоянии хода коня, то DE можно заменить через DL и цепь ходов обратится в

т. е. вторая половина цепи будет пройдена в обратном порядке.

То же самое относится и к тому случаю, когда какая-нибудь клетка, кроме второй, сообщается ходом коня с первой. Итак, цепь (или ряд ходов) можно видоизменять, не разрывая ее.

Число путей, которыми конь может обойти доску и которые можно найти указанными выше приемами, не бесконечно. Но оно настолько огромно, что трудно его представить.

Эта задача известна по крайней мере с XVIII века. Леонард Эйлер посвятил ей большую работу «Решение одного любопытного вопроса, который, кажется, не подчиняется никакому исследованию» (датируется 26 апреля 1757 года). В письме к Гольдбаху он сообщал:

…Воспоминание о предложенной когда-то мне задаче послужило для меня недавно поводом к некоторым тонким изысканиям, в которых обыкновенный анализ, как кажется, не имеет никакого применения… Я нашел, наконец, ясный способ находить сколько угодно решений (число их, однако, не бесконечно), не делая проб.

Содержание

Формулировка задачи

Количество всех замкнутых маршрутов коня (гамильтоновых циклов) без учёта направления обхода равно 13 267 364 410 532 [1] (количество замкнутых маршрутов с учётом направления в два раза больше). В то же время задача подсчёта всех возможных незамкнутых маршрутов значительно сложнее и не решена до сих пор. Известно, [2] что количество незамкнутых маршрутов не превышает числа сочетаний

$\binom<168><63>\approx 1.2\cdot 10^<47>$
.

Студентами Псковского политехнического института в 2011 году подсчитано количество обходов поля 7 на 7, оно составило 167 883 607 248. И показано, что количество обходов на поле 8 на 8 не должно превысить
.

Методы решения

Метод Эйлера

Рассмотрим в качестве примера следующий маршрут:

55	58	29	40	27	44	19	22
60	39	56	43	30	21	26	45
57	54	59	28	41	18	23	20
38	51	42	31	8	25	46	17
53	32	37	a	47	16	9	24
50	3	52	33	36	7	12	15
1	34	5	48	b	14	c	10
4	49	2	35	6	11	d	13

57	54	29	40	27	44	19	22
52	39	56	43	30	21	26	45
55	58	53	28	41	18	23	20
38	51	42	31	8	25	46	17
59	32	37	a	47	16	9	24
50	3	60	33	36	7	12	15
1	34	5	48	b	14	c	10
4	49	2	35	6	11	d	13

Метод Вандермонда

Вандермонд попытался свести задачу к арифметической. Для этого он обозначал маршрут коня по доске в виде последовательности дробей $\frac<x><y>$
, где x и y — координаты поля на доске. Очевидно, что в последовательности дробей, соответствующей ходам коня, разность числителей двух соседних дробей может быть только 1 или 2, при том, что разность их знаменателей составляет соответственно 2 или 1. Кроме того, числитель и знаменатель не могут быть меньше 1 и больше 8.

Правило Варнсдорфа

Примечательные маршруты

Маршрут Яниша

50	11	24	63	14	37	26	35
23	62	51	12	25	34	15	38
10	49	64	21	40	13	36	27
61	22	9	52	33	28	39	16
48	7	60	1	20	41	54	29
59	4	45	8	53	32	17	42
6	47	2	57	44	19	30	55
3	58	5	46	31	56	43	18

Примечателен маршрут коня, найденный К. Я. Янишем: он образует полумагический квадрат, а при повороте доски на 180° первая половина маршрута (номера с 1 до 32) переходит во вторую (номера с 33 по 64).

Маршрут, найденный шахматным автоматом

Шахматный автомат нашёл замкнутый маршрут коня, изображенный на диаграмме справа.

Мнемоническое стихотворение

Обойти конём все шахматные клетки и ни разу не побывать дважды на одной и той же, к тому же сделать это «вслепую», начав или закончив на любой клетке по желанию «зрителя», можно благодаря стихотворению: [3]

Два Вечера Цеплявшиеся Шишки
Артист Писал, Бездонна Синева.
Дорожный Шлак Целуют Червячишки,
Еще Покрыта Флоксами Трава.

Дымится Чай Эффектней Шоколада,
Фарфоры Чашек Достаются Трем,
Блондинке Девушка Дана Отрада
Форшмак Делить Холодным Острием.

Жена, Толкая Хилую Подругу,
Желает Сняться Этим Выходным,
Ценя Сама Арктическую Вьюгу,
Бросает Шар Арбуза Четверым.

Цикад Пяток, Едва Чревовещая,
Дарует Дрему Фикусам Окна.
Хотя Довольны Жаждавшие Чая,
Хозяин Шумно Жертвует Вина.

Фокстротами Шесть Девушек Пленились,
Эстрадных Танцев Фантастичней Па,
Едва Ступающий Цыпленок Вылез,
А Селезень Блуждающий Пропал.

Алеет Тело Бронзовой Осины,
Царит Теней Ажурная Длина.
Беззвучней, Чем Автомобиля Шины,
Болоту Ветер Дарит Семена.

Первые буквы задают координаты ходов:

Алеет Осень = А1; Ценными Дарами = С2; и т. д.

Обобщение на произвольные доски

Для неквадратных досок обход конём существует только при выполнении следующих условий: если одна сторона доски равна 3, то другая должна быть либо 4, либо не меньше 7; если же обе стороны больше 3, то обход коня возможен на всех досках, кроме 4×4. В частности, для квадратных досок решение существует при размерах 5×5 и более.

По цене конь примерно равен слону или трём пешкам

Ход коня похож на кириллическую (русскую) букву «Г» или латинскую букву «L». Конь перемещается на два поля вверх или вниз, а затем на поле вбок, либо на два поля вбок, а затем на одно поле вверх или вниз. Конь меняет цвет поля, на котором стоит, с каждым ходом. Например, если конь стоит на белом поле, после хода он окажется на чёрном поле.

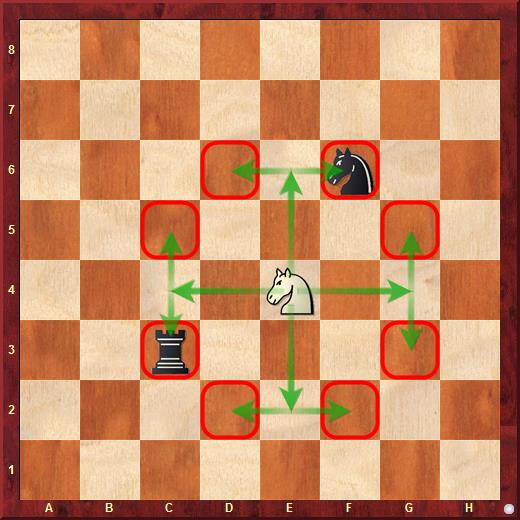
Посмотрите на стрелки и постарайтесь запомнить, как ходит конь в шахматах. Конь может попасть на любое из восьми полей отмеченных красным цветом. Если на поле находится вражеская фигура или пешка, то конь может её забрать. В данном случае белый конь может забрать чёрного коня или ладью

В книге «Куда идет король» Виктор Хенкин рассказал забавный случай:

— Как вы оцениваете мою игру? — спросил однажды у чемпиона мира X. Капабланки какой-то молодой человек.
— Вы играли неплохо, — вежливо ответил Капабланка. — Но почему вы не сделали ни одного хода конями?
— А я не знаю, как они ходят, — признался «шахматист»…

Конь — удивительная шахматная фигура, он может перепрыгивать через другие фигуры и пешки!

Белый конь находится в окружении друзей и врагов, но это никак не может помешать ему сходить на любое из восьми полей отмеченных зелёным цветом

Манёвренность коней

Ни одна другая фигура, переставленная на угловое поле, не теряет в подвижности столько, сколько теряет конь.

Сравните маневренность обоих коней на диаграмме. Конь с h1 обстреливает всего два поля, то есть в четыре раза меньше, чем его напарник с d5. Поэтому сила коня, находящегося в центре доски, резко возрастает, и это обстоятельство необходимо во время игры учитывать

Если коня с поля h1 переместить на h4, то он будет контролировать 4 поля, но это все равно в два раза меньше, чем в центре. В этой связи вспомним высказывание знаменитого немецкого шахматиста Зигберта Тарраша:

«Конь на краю доски всегда стоит плохо».

Из любого правила бывают исключения — иногда конь на краю доски расположен идеально.

Что любят кони?

Мы уже знаем, что слоны любят открытые диагонали, т.е. открытые позиции. Поскольку кони могут прыгать через другие фигуры, их сила возрастает в закрытых позициях, где дальнобойность других фигур (ферзей, ладей и слонов) ограничена.

В книге «Учебник шахматной игры» Хосе Рауль Капабланка написал:

Сила коней падает по мере размена фигур на доске.

Кроме закрытых позиций, кони любят безопасность, поэтому они всегда рады занять форпост — поле в лагере противника, где коня не могут атаковать вражеские пешки.

Белый конь занял форпост на поле e6 и доставляет много хлопот чёрным

Вилка конём

В отличие от других фигур, конь не действует прямолинейно, поэтому коневая вилка зачастую оказывается полной неожиданностью. Много партий было проиграно после нападения коня одновременно на несколько фигур.

Белый конь напал на две фигуры (двойная вилка) — короля и ладью. Король вынужден спасаться от шаха и белые забирают ладью

Позиция из партии Греко — NN (1620). Конь напал сразу на три фигуры (тройная вилка): короля, ферзя и ладью. После отхода короля, конь заберет наиболее ценную фигуру чёрных, т.е. ферзя

Задачи на тему «Вилка конём»

Настала пора опробовать на практике полученные знания и решить десять интерактивных задач на тему «Вилка конём». Будьте внимательны при решении задачи №10.

Термин "гиппофобия" - боязнь лошадей, применим и к шахматам! Некоторые шахматисты боятся наличия у противника коней. Шахматная гиппофобия приводит к необдуманному размену своих фигур на коней, например, слона на коня.

Что мы знаем о коне?

Основное отличительное свойство — смена цвета поля при каждом ходе.
Король противника не может прикрыться никакой фигурой от атаки конём или взять его (если только конь не займёт поле, находящееся под боем короля).
Конь — единственная фигура, способная самостоятельно угрожать ферзю противника, не рискуя попасть под угрозу со стороны последнего.
Конь способен перескакивать через другие фигуры, как своего цвета, так и чужого.
Из предыдущего пункта следует, что конь является единственной фигурой, которой игрок при желании может сделать первый ход в начале партии (кроме пешки).

В заключение добавим, что именно конём ставится спёртый мат.

Читайте также: